PCR

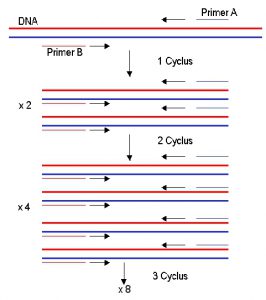
Um bestimmte Bereiche des Genoms (und damit der DNA) zu „vermehren“ setzt man die PCR (polymerase chain reaction) ein. Hierbei werden kleine DNA-Stücke eingesetzt (Primer), die an die DNA binden. Man kann durch den Einsatz von Enzymen die DNA-Bereiche die zwischen den Primern liegen „vermehren“.

Das Erbgut (DNA) besteht aus zwei Strängen die sich wie eine Leiter aneinander lagern. Wenn man die DNA erhitzt, werden diese Stränge voneinander getrennt. Beim Abkühlen können sich die Primer an diese Stränge lagern. Ein Enzym kann nun aus dem einen Strang und dem Primer wieder diese Leiter synthetisieren. Somit erhält man nach einem dieser Cyclen die doppelte Menge der DNA, die zwischen diesen beiden Primern liegt. Im nächsten Cyclus wird die DNA wieder verdoppelt und im nächsten Cyclus wieder. Es ist vergleichbar mit dem Schachbrett und dem Reiskorn. Auf das erste Feld kommt ein Korn, auf das zweite 2, auf das dritte 4, auf das vierte 8 usw. Dadurch erhält man nach einigen Cyclen die millionenfache Menge an DNA. Somit lassen sich auch kleinste Mengen analysieren. Ausserdem werden nur die DNA-Teile vervielfältigt, welche zwischen den beiden Primern liegen. Durch die Wahl der Primer kann man also bestimmen, welche DNA-Teile vervielfältigt werden.

Der indische Herrscher Shihram tyrannisierte seine Untertanen und stürzte sein Land in Not und Elend. Um die Aufmerksamkeit des Königs auf seine Fehler zu lenken, ohne seinen Zorn zu entfachen, schuf Dahirs Sohn, der weise Brahmane Sissa, ein Spiel, in dem der König als wichtigste Figur ohne Hilfe anderer Figuren und Bauern nichts ausrichten kann. Der Unterricht im Schachspiel machte auf Shihram einen starken Eindruck. Er wurde milder und ließ das Schachspiel verbreiten, damit alle davon Kenntnis nähmen. Um sich für die anschauliche Lehre von Lebensweisheit und zugleich Unterhaltung zu bedanken, gewährte er dem Brahmanen einen freien Wunsch. Dieser wünschte sich Weizenkörner: Auf das erste Feld eines Schachbretts wollte er ein Korn, auf das zweite Feld das Doppelte, also zwei, auf das dritte wiederum die doppelte Menge, also vier und so weiter. Der König lachte und war gleichzeitig erbost über die vermeintliche Bescheidenheit des Brahmanen.

Als sich Shihram einige Tage später erkundigte, ob Sissa seine Belohnung in Empfang genommen habe, musste er hören, dass die Rechenmeister die Menge der Weizenkörner noch nicht berechnet hätten. Der Vorsteher der Kornkammer meldete nach mehreren Tagen ununterbrochener Arbeit, dass er diese Menge Getreidekörner im ganzen Reich nicht aufbringen könne. Auf allen Feldern eines Schachbretts zusammen wären es 2⁶⁴-1 oder 18.446.744.073.709.551.615 (≈ 18,45 Trillionen) Weizenkörner. Nun stellte er sich die Frage, wie das Versprechen eingelöst werden könne. Der Rechenmeister half dem Herrscher aus der Verlegenheit, indem er ihm empfahl, er solle Sissa ibn Dahir ganz einfach das Getreide Korn für Korn zählen lassen. Quelle: https://de.wikipedia.org/wiki/Sissa_ibn_Dahir

Um die Menge etwas deutlich zu machen:

Angenommen, der Weizen soll in LKWs mit einer Nutzlast von 8840 kg verladen werden, die eine Länge von 7,6 Metern aufweisen, dann passen in einen Transporter 176.800.000 Getreidekörner. Insgesamt benötigt man daher ca. 104 Milliarden Transporter, um alles zu verladen. Stoßstange an Stoßstange aufgestellt, ergeben diese Transporter eine Strecke von ca. 793 Millionen km; bei einem angenommenen Erdumfang von 40.000 km ergibt das insgesamt fast 20.000 Erdumrundungen (oder 5,3 mal die Entfernung von der Erde bis zur Sonne). Quelle: https://www.waldorf-ideen-pool.de/Schule/faecher/mathematik/mittelstufe/potenzrechnung/weizenkornlegende—schachbrett

Hier ein Bild eines echten genetischen Fingerabdrucks.